What is a strong interval? Without going into a lot of theory, we can describe it like this:

A strong interval is one that is easy to get into tune, or alternately, one that will quickly tell you if you’ve moved a note a little out of place.

   Clearly, the strongest of all are the unison and the octave, which are used to tune the guitar for that very reason. But octaves and unisons are not harmonic intervals because they contain only one note.

   After the octave and the unison, the strongest interval is the perfect fifth – the distance between the root and the fifth note of the major scale – which is a harmonic interval because it has two different notes. Violinists use the strength of the perfect fifth when they tune by sounding both notes together, adjusting one until they hear an accurate perfect fifth. The inversion of the perfect fifth, the perfect fourth – the 4^th note of the major scale from the root – is weaker, and it is very unreliable to tune a guitar with, even though it is the interval between four of the strings.

   You invert an interval by flipping it upside down; for example C to E is a major third, while its inversion, E to C, is a minor sixth. So the perfect fifth is the best place to start building a stable chord (and a primary reason many metal bands play “5” chords as the foundation of their rhythm parts – it sounds good “naturally”).

   To make even the simplest complete chord, you need another note, but which one? If you add another perfect fifth, keeping the club exclusive, you get something like the chords in Ex. 1, which sound like tune-up time at a Country hoedown. If you bring the same notes closer together, as in Ex. 2, you introduce the dissonant major second interval and produce chords that are not simple and basic. At the time of the first millennium, such sounds were accepted, but that was a long time ago.

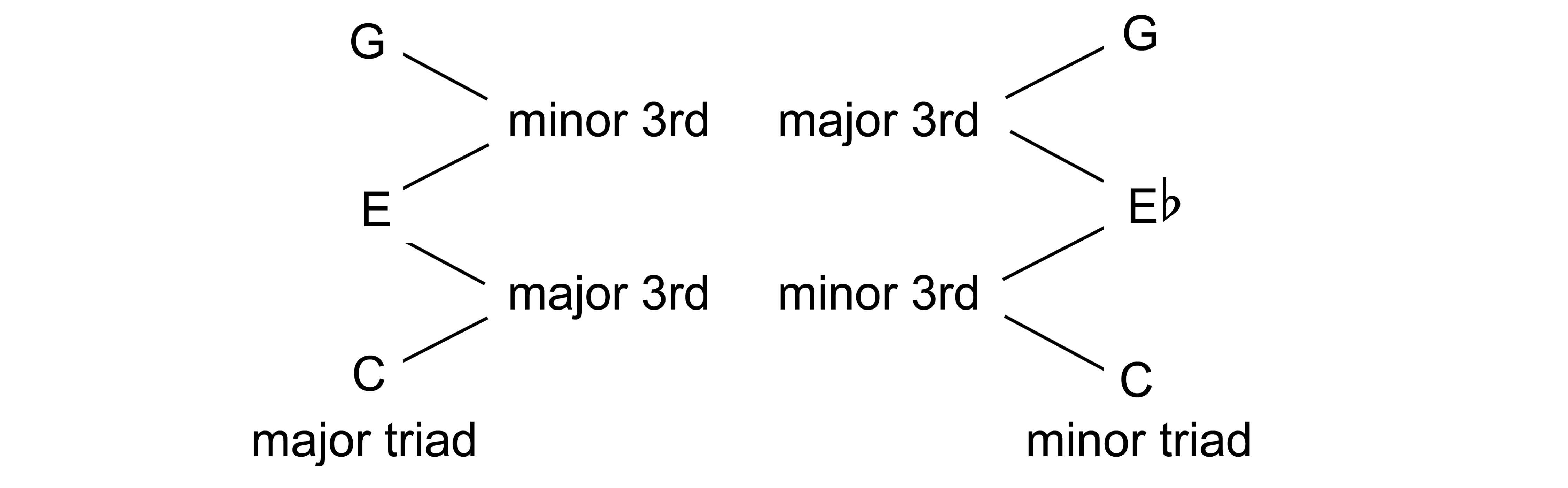
   If you take the perfect fifth as what it is – strong and firm, but empty sounding – you’ll realize that its effect needs to be softened and made more everyday friendly, more accessible. This can be accomplished by dividing it into two thirds within a sort of ice-breaker, as in Ex. 3. In Ex. 3a, there’s a major third – four half-step distance – at the bottom of the pile and a minor third (a three half-step distance) at the top; in Ex. 3b, the order is reversed, but both types of chords sound pleasant and familiar. What you have produced are so familiar that they are called the “common chords,” and since they have three notes, they are known as triads. They are further named by the lower of the two thirds they contain, so the first type is the major triad and the second is the minor triad. Listen carefully to these chords and notice that the minor triad has a softer, darker sound than the major.

   Ex. 4 shows several triads. Identify them as either major or minor and watch for the three booby traps that are neither major nor minor (don’t peek at the answers in the last paragraph). Next, write down the major and minor triads based on every chromatic note from C to B, including the enharmonic tones (single notes having two names, such as C# and Db. If you feel brave enough, include Fb and Cb.

   Here are the answers to Ex. 4: (a) F major, (b) C# minor, (c) G minor, (e) D major, (f) Ab major, (h) A major, (i) E minor, (j) B minor, (k) Eb minor, (m) Db major. Letters (d), (g), and (l) are neither major nor minor; in future installments, you’ll learn what they are, plus a whole lot more.